
정렬 알고리즘
정렬이란?
정렬(sorting)이란 이름, 학번, 학점 등의 키를 항목값의 대소 관계에 따라 데이터 집합을 일정한 순서로 바꾸어 늘어놓는 작업을 말한다.
오름차순(ascending order) - 값이 작은 데이터를 앞쪽에 늘어놓는 것을 의미한다.
내림차순(descending order) - 값이 큰 데이터를 앞쪽에 늘어놓는 것을 의미한다.

정렬 알고리즘의 안정성
정렬 알고리즘은 안정적인(stable) 알고리즘과 그렇지 않은 알고리즘으로 나눌 수 있다. 안정적인 알고리즘은 정렬한 후에도 순서가 변하지 않고 값이 같은 원소의 순서가 정렬 후에도 유지되는 것을 말한다. 반면 그렇지 않은 정렬 알고리즘은 정렬 후에 원래 순서가 유지된다는 보장을 할 수 없다.
내부 정렬과 외부 정렬
하나의 배열에 작업할 수 있는 경우 내부 정렬(internal sorting)을 사용하고, 그렇지 않은 경우에는 외부 정렬(external sorting)을 사용한다.
🎈 지금 여기 티스토리에 올리는 정렬은 모두 내부 정렬입니다.
정렬 알고리즘의 핵심은 교환, 선택, 삽입이다.
정렬 알고리즘은 데이터를 교환, 선택, 삽입하면서 정렬을 완료한다. 대부분의 정렬 알고리즘은 이 3가지를 응용하고 있으며, 앞으로 다룰 8가지의 정렬 알고리즘에서도 자주 등장하는 핵심적인 개념이다.
버블, 단순 선택, 단순 삽입, 셀, 퀵, 병합, 힙, 도수 정렬 등이 있다.
버블 정렬
버블 정렬(bubble sort)은 이웃한 두 원소의 대소 관계를 비교하여 필요에 따라 교환을 반복하는 알고리즘으로, 단순 교환 정렬이라고도 한다.
버블 정렬 알아보기
먼저 오른쪽 끝에 있는 두 원소 9와 8에 주목해야 한다. 이때 배열을 오름차순으로 정렬한다면 왼쪽의 값(9)이 오른쪽의 값(8)과 같거나 작아야 한다.
| 6 | 4 | 3 | 7 | 1 | 9 | 8 |
따라서 9와 8을 교환하면 다음과 같이 된다. 이제 다음 비교 대상인 1과 8에 주목한다. 1은 8보다 작으므로 교환할 필요가 없다.
| 6 | 4 | 3 | 7 | 1 | 8 | 9 |
:
:
:
이러한 일련의 비교, 교환 과정을 패스(pass)라고 한다.

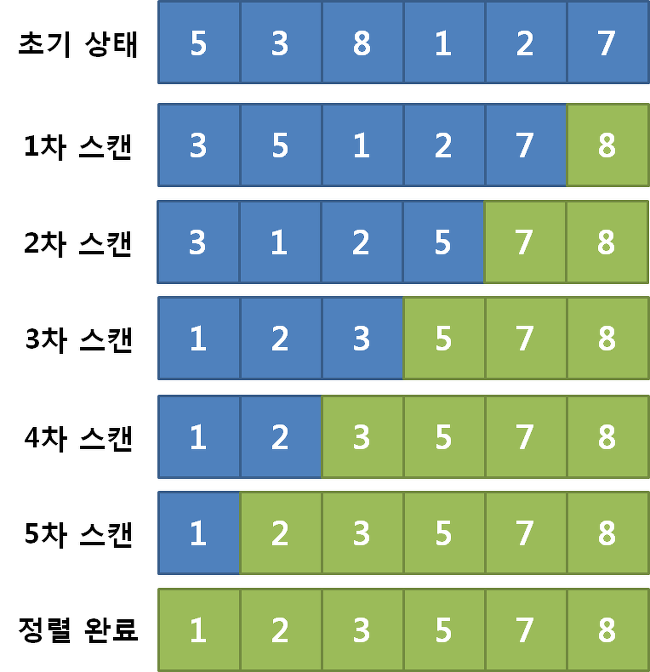
앞에서 살펴보듯 정렬을 끝내려면 n-1번을 수행해야하고 이때 n-1번인 이유는 n-1개 원소의 정렬이 끝나면 마지막 원소는 이미 끝에 놓이기 때문이다.
📄버블 정렬(bubble sort)은 액체 속의 공기 방울이 가벼워서 위로 보글보글 올라오는 모습에 착안해서 붙인 이름입니다.
버블 정렬 프로그램
# 버블 정렬 알고리즘 구하기
from typing import MutableSequence
def bubble_sort(a):
#버블 정렬
n = len(a)
for i in range(n-1):
for j in range(n-1, i, -1): #패스
if a[j-1] > a[j]: #크기를 비교해서 자리를 바꿔주는 작업
a[j-1],a[j] = a[j],a[j-1]
if __name__ == '__main__':
print('버블 정렬을 수행합니다.')
num = int(input('원소 수를 입력하세요.: '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
bubble_sort(x) #배열 x를 버블 정렬
print("오름차순으로 정렬했습니다.")
for i in range(num):
print(f"x[{i}] = {x[i]}")n-1만큼인 이유는 위에 설명했듯 마지막에 이미 원소가 끝에 놓이기 때문이다.
단순 선택 정렬 (straight selection sort)
단순 선택 정렬(straight selection sort)은 가장 작은 원소부터 선택해 알맞은 위치로 옮기는 작업을 반복하며 정렬하는 알고리즘이다.
단순 선택 정렬 알아보기
| 6 | 4 | 8 | 3 | 1 | 9 | 7 |
가작 장은 원소부터 정렬하므로 가장 작은 원소 1에 주목한다.
| 1 | 4 | 8 | 3 | 6 | 9 | 7 |
1은 배열의 맨 앞에 위치해야 하므로 맨 앞의 원소 6과 교환한다. 교환한 다음 원소의 배열 상태는 다음과 같다.
| 1 | 3 | 8 | 4 | 6 | 9 | 7 |
가장 작은 원소인 1이 맨 앞에 위치했고, 이어서 두 번째로 작은 원소인 3을 주목한다. 원소 3과 맨 앞에서 두 번째 원소인 4를 교환하면 다음과 같이 두 번째 워너소까지 정렬이 완료된다.
| 1 | 3 | 4 | 8 | 6 | 9 | 7 |
다음으로 세 번째 작은 원소인 4를 주목한다. 원소 4와 맨 앞에서 세 번째 원소인 8을 교환하면 다음과 같이 세 번째 원소 정렬이 완료된다.
이런식으로 계속 정렬해나가는 방법이 단순 선택 정렬이다.
1. 아직 정렬하지 않은 부분에서 값이 가장 작은 원소 a[min]을 선택한다.
2. a[min]과 아직 정렬하지 않은 부분에서 맨 앞에 있는 원소를 교환한다.
이 과정을 n-1번 반복하면 정렬하지 않은 부분이 없어지면서 전체 정렬을 완료한다. 이 알고리즘의 개요는 다음과 같다.
for i in range(n-1):
min #a[i]...a[n-1]에서 키값이 가장 작은 원소의 인덱스
a[i]와 a[min]의 값을 교환합니다.#단순 선택 정렬 알고리즘 구현하기
from typing import MutableSequence
def selection_sort(a):
#단순 선택 정렬
n = len(a)
for i in range(n-1):
min = i #정렬할 부분에서 가장 작은 원소의 인덱스
for j in range(i+1, n):
if a[j] < a[min]:
min =j
a[i],a[min] = a[min],a[i] #정렬할 부분에서 맨 앞의 원소와 가장 작은 원소를 교환단순 선택 정렬 알고리즘의 원솟값을 비교하는 횟수는 (n**-n)/2번이다. 그러나 이 알고리즘의 경우엔 이웃하지 않고 떨어져있는 원소를 교환하기 때문에 안정적이지 않다.
단순 삽입 정렬 (straight insertion sort)
단순 삽입 정렬(straight insertion sort)은 주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘이다. 단순 선택 정렬과 비슷해보이지만 값이 가장 작은 원소를 선택하지 않는다는 점이 다릅니다.
단순 삽입 정렬 알아보기
단순 삽입 정렬은 카드를 한 줄로 늘어놓을 때 사용하는 방법과 비슷한 알고리즘이다. 다음 배열을 예로 들어 단순 삽입 정렬하는 방법을 살펴보자
| 6 | 4 | 1 | 7 | 3 | 9 | 8 |
단순 삽입 정렬은 두 번째 원소인 4부터 주목하여 진행한다. 4는 6보다 앞쪽에 위치해야 하므로 맨 앞에 삽입한다. 이 상태에서 6을 오른쪽으로 옮기면 다음과 같다.
| 4 | 6 | 1 | 7 | 3 | 9 | 8 |
다음으로 세 번째 원소인 1에 주목한다. 1은 4보다 앞쪽에 위치해야 하므로 맨 앞에 삽입을 해야 한다. 이 상태에서 4, 6을 오른쪽으로 옮기면 다음과 같다.
| 1 | 4 | 6 | 7 | 3 | 9 | 8 |
그 이후에도 계속해서 같은 작업을 수행하면 n-1번의 반복하면서 정렬이 완료된다.
아직 정렬되지 않은 부분의 맨 앞 원소를 정렬된 부분의 알맞은 위치에 삽입한다.
i를 1,2,,,,n-1까지 1씩 증가시키면서 인덱스 i의 원소를 꺼내 알맞은 위치에 삽입한다. 따라서 알고리즘의 개요는 다음과 같다.
for i in range(1,n):
tmp <- a[i]를 넣습니다.
tmp를 a[0], ..., a[i - 1]의 알맞은 위치에 삽입합니다.
'알맞은 위치에 삽입'하는 과정을 생각해보자
'자료구조와 알고리즘 > 자료구조와 함께 배우는 알고리즘' 카테고리의 다른 글
| [자료구조와 함께 배우는 알고리즘][정렬 알고리즘] - 퀵 정렬 (0) | 2021.10.07 |
|---|---|
| [자료구조와 함께 배우는 알고리즘][정렬 알고리즘] - 셸 정렬 (0) | 2021.10.06 |
| Python - 재귀 알고리즘(부제: 재귀 알고리즘이 무엇인지 알아보고 하노이의 탑을 알아보자) (0) | 2021.07.15 |
| Phython - 스택과 큐(부제: 스택과 큐를 알아보며 예외처리가 무엇 인지를 살펴보자!) (0) | 2021.07.05 |
| Python - 검색 알고리즘(부제: 검색 알고리즘이 무엇인지 살펴보고, 선형 검색, 이진 검색, 해시법을 알아보자) (0) | 2021.06.26 |