
(이코테 2021 강의 몰아보기) 6. 다이나믹 프로그래밍
[한빛미디어] 이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저) 이 영상은 라이브 강의 때 진행했던 내용을 보완하여 1080 HD로 재녹화한 버전이며, 타임라인은 다음과 같습니다. 28강: 다
youtu.be

<문제: 개미 전사>





#DP 테이블의 값을 갱신한다고 생각하고 진행한다.

#개미 전사
n = int(input()) #식량창고의 개수
array = list(map(int,input().split())) #식량창소에 저장된 식량의 개수 K
#dp 테이블 초기화
d = [0] * 100
#다이나믹 프로그래밍 진행(보텀업)
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
d[i] = max(d[i-1], d[i-2] +array[i])
#현재 i값이 i-2 + i일 때, 현재값 바로 직전의 i-1값이 더 크면 i-1을 아니라면 i-2 +i를 저장한다.
print(d[n-1]) #array[0]~ array[n-1]<문제: 효율적인 화폐 구성>







import sys
input = sys.stdin.readline
n, m = map(int,input().split())
coin = []
for _ in range(n):
coin.append(int(input()))
#계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [10001]*(m+1)
#다이나믹 프로그래밍 진행(보텀업)
d[0] = 0
#점화식에 따라 다이나믹 프로그래밍 진행
for i in range(n): # i == 화폐단위
for j in range(coin[i],m+1): #j == 금액
if d[j - coin[i]] != 10001: #(i-k)원을 만드는 경우가 존재하는 경우
d[j] = min(d[j],d[j-coin[i]]+1)
#계산된 결과 출력
if d[m] == 10001: #최종적으로 M원을 만드는 방법이 없는 경우
print(-1)
else:
print(d[m])<문제: 금광>
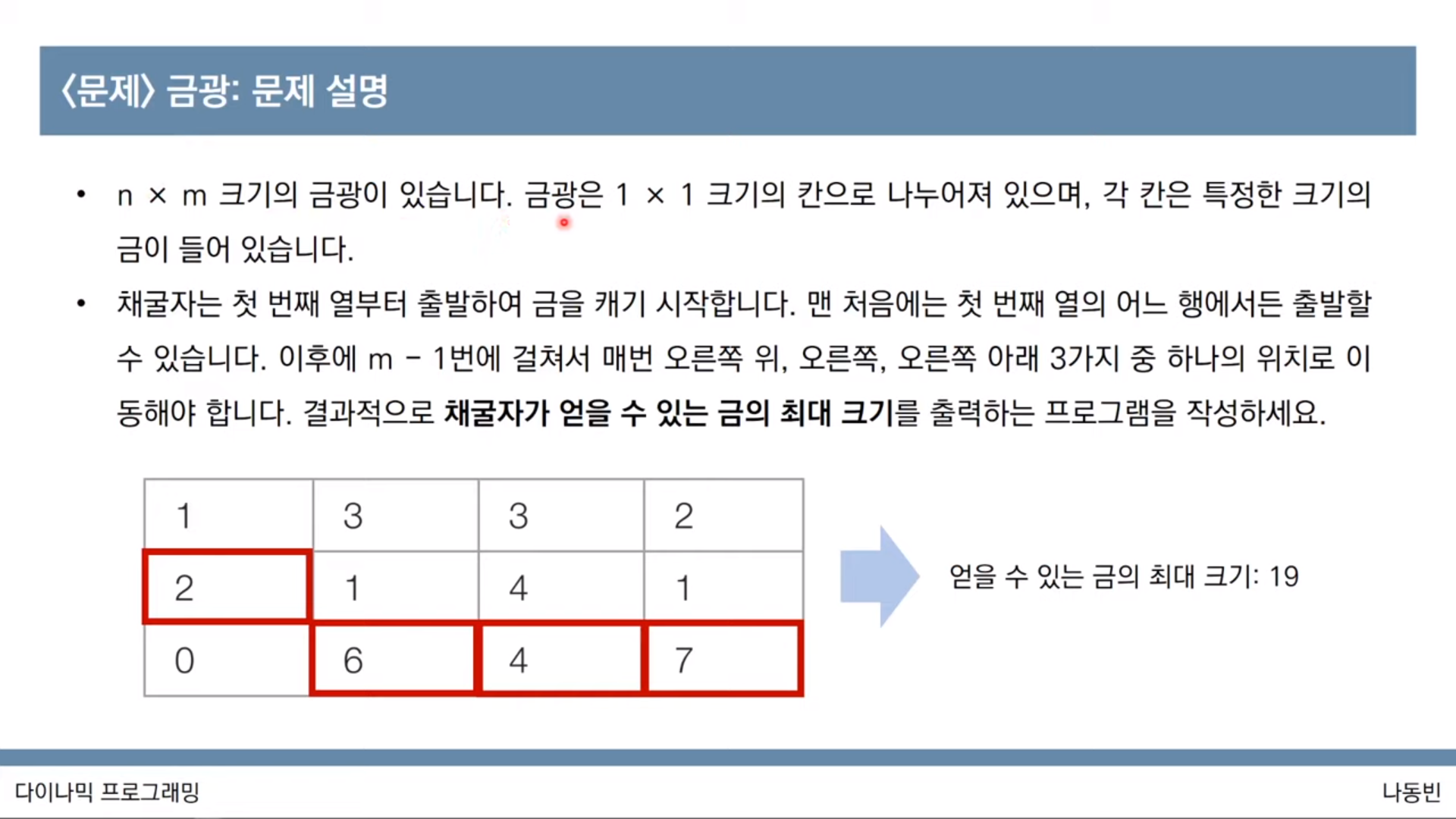




import sys
input = sys.stdin.readline
for tc in range(int(input())):
#금광 정보 입력
n, m = map(int,input().split())
array = list(map(int,input().split()))
#다이나믹 프로그래밍을 위한 2차원 DP테이불 초기화
dp = []
index = 0
for i in range(n):
dp.append(array[index:index+m]) #쭉 입력받은 것을 2차원 배열로 담기 위한 작업 m단위로 슬라이싱해서 dp 테이블에 2차원 테이블로 넣어줄 수 있게 한다.
index += m
#다이나믹 프로그래밍 진행
for j in range(1, m): #열 확인
for i in range(n): #열마다 행 확인
#왼쪽에서 위에서 오는 경우
if i == 0: #인덱스가 벗어나는 경우
left_up = 0
else:
left_up = dp[i-1][j-1]
#왼쪽 아래에서 오는 경우
if i == n - 1: #인덱스가 벗어나는 경우
left_down = 0
else:
left_down = dp[i+1][j-1]
#왼쪽에서 오는 경우
left = dp[i][j-1]
dp[i][j] = dp[i][j] + max(left_up, left_down, left)
result = 0
for i in range(n):
result = max(result, dp[i][m-1])
print(result)<문제: 병사 배치하기>

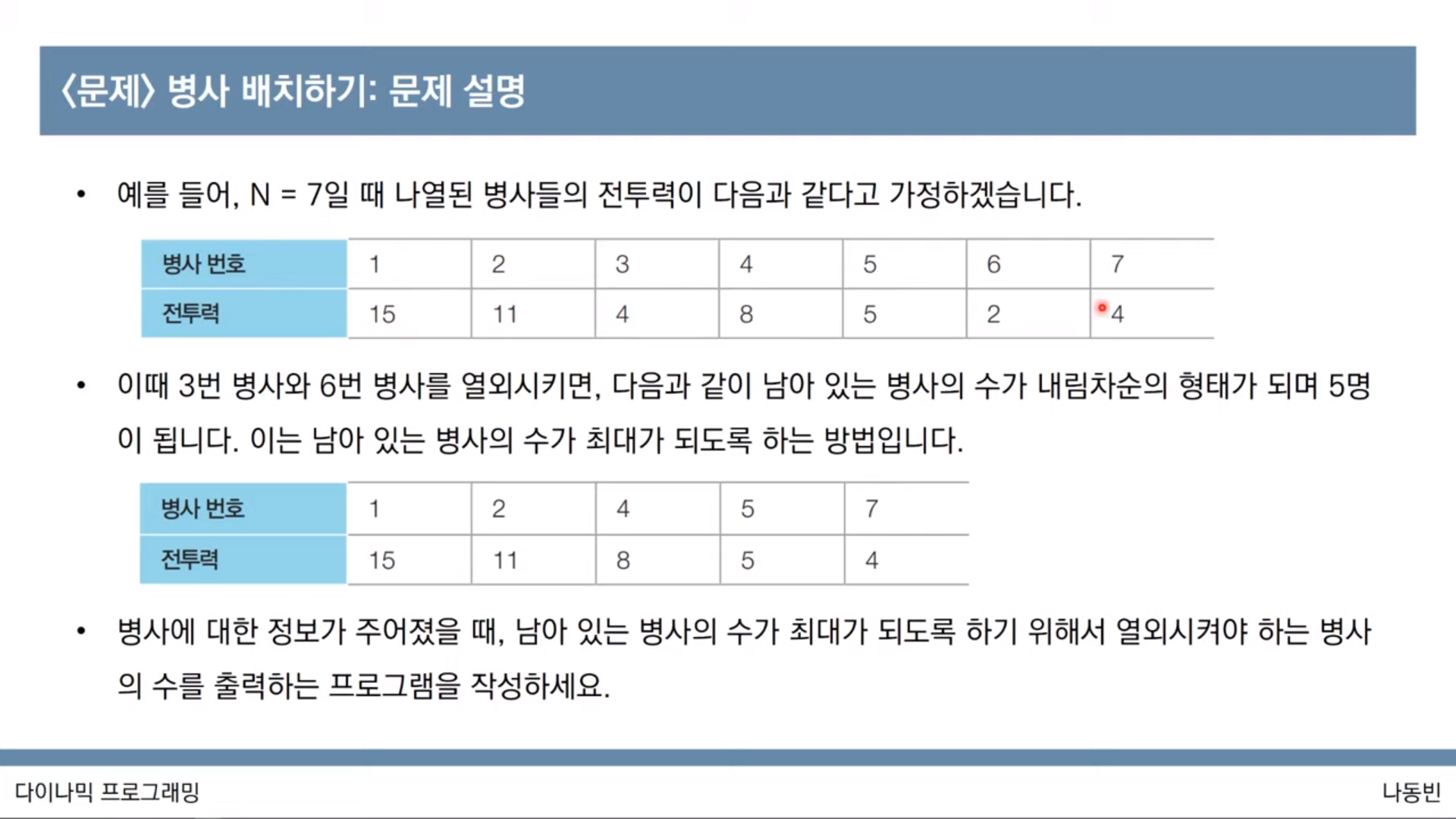
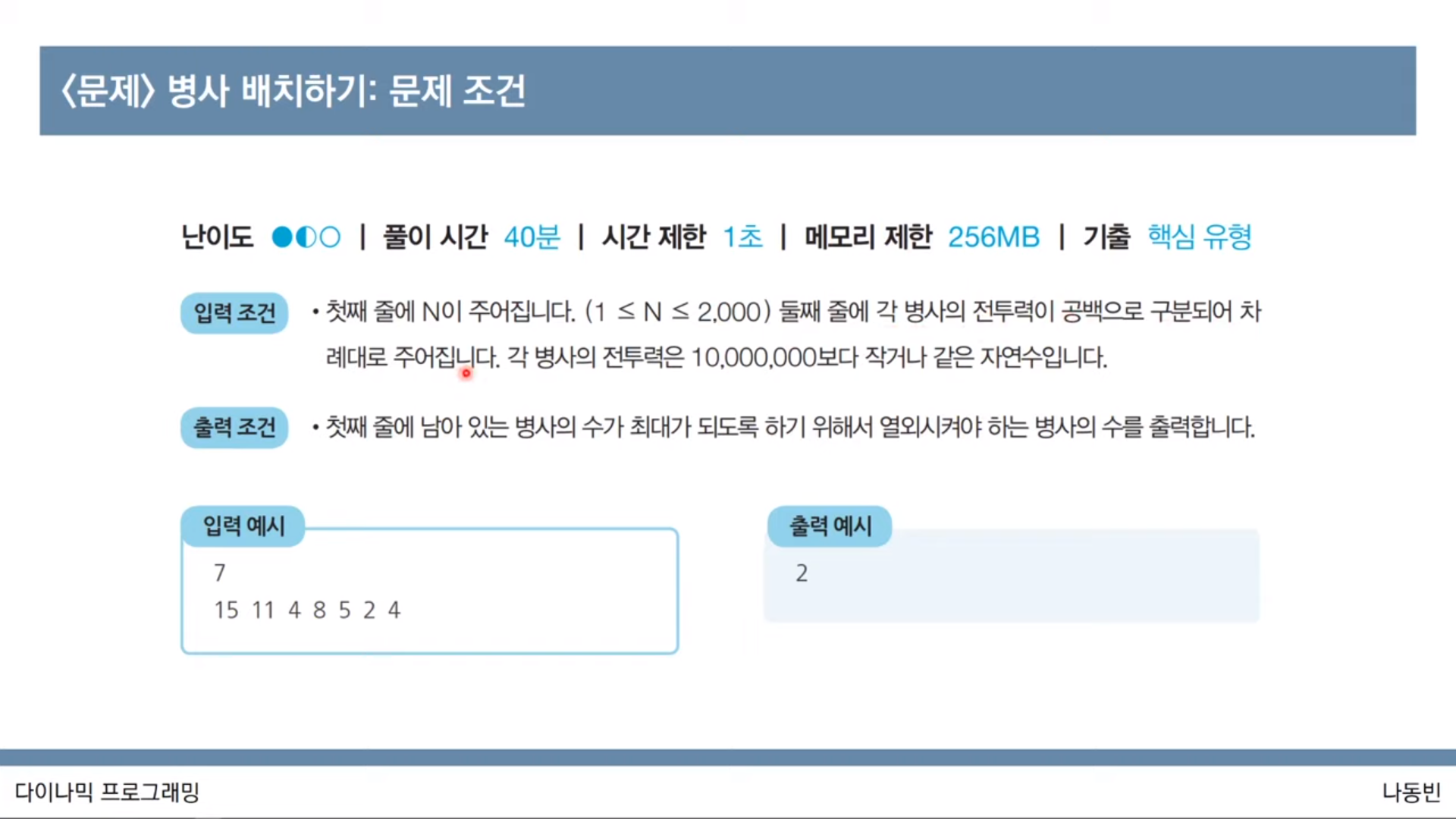


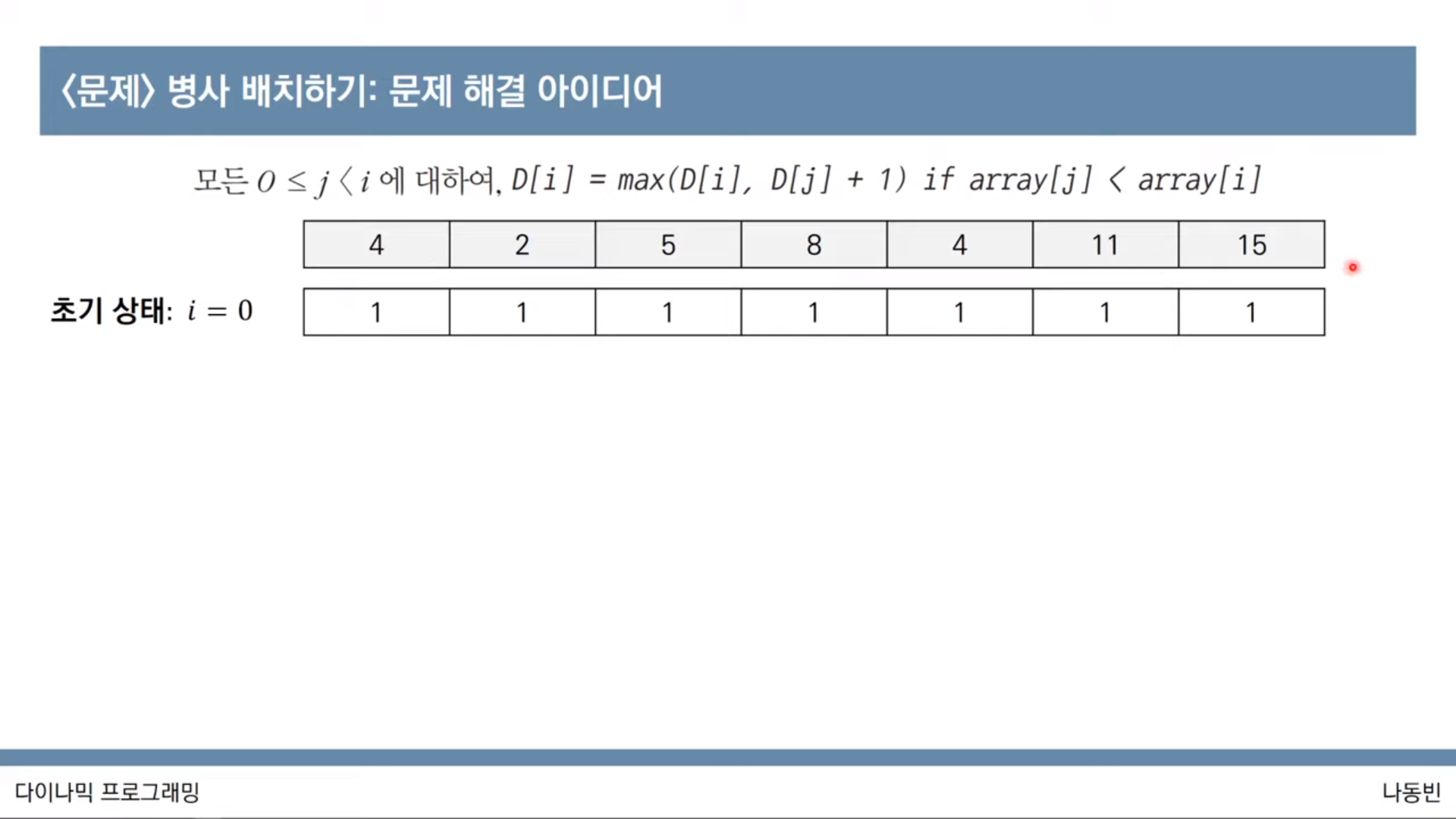
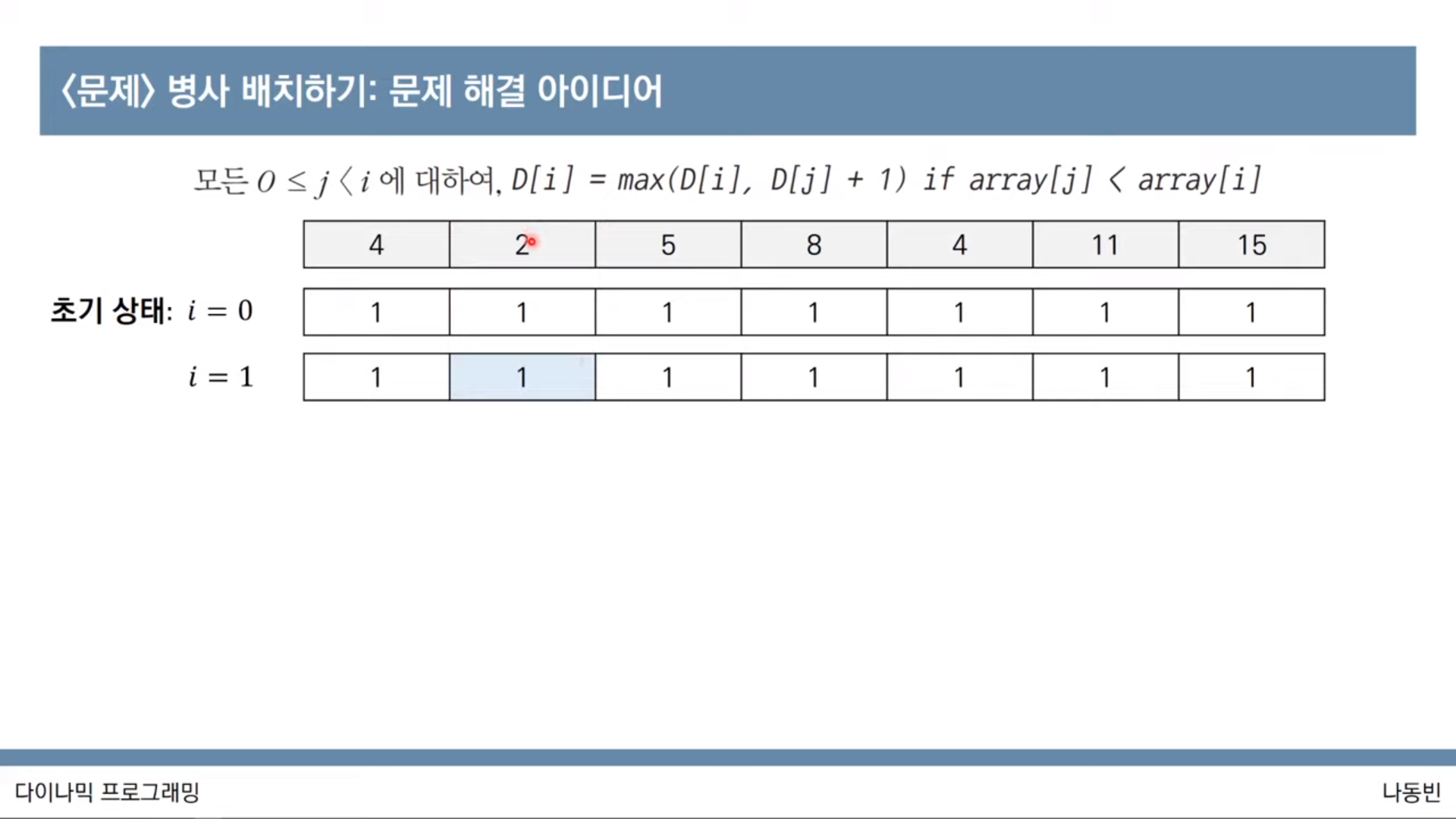


#LIS
import sys
input = sys.stdin.readline
n = int(input())
array = list(map(int,input().split()))
#순서를 뒤집어 최장 증가 부분 수열 문제로 변환
array.reverse()
#다이나믹 프로그래밍을 위한 1차원 DP 테이블 초기화
dp = [1] * n
#가장 긴 증가하는 부분 수열(LIS) 알고리즘 수행
for i in range(1,n):
for j in range(0,i):
if array[j] < array[i]:
dp[i] = max(dp[i],dp[j] +1)
#열외해야 하는 병사의 최소 수를 출력
print(n-max(dp))'자료구조와 알고리즘 > 이것이 취업을 위한 코딩테스트다' 카테고리의 다른 글
| 자료구조 - 우선순위 큐 (부제: 우선순위 큐와 힙은 어떤 관계일까?) (0) | 2021.09.17 |
|---|---|
| 알고리즘 - 최단 경로 알고리즘(Shortest algorithm) / 다익스트라 알고리즘 (0) | 2021.09.15 |
| 알고리즘 - 동적 프로그래밍 알고리즘(Dynamic programming algorithm) (0) | 2021.09.01 |
| 알고리즘 - 이진 탐색 알고리즘 (Binary Search algorithm) 기초 문제 풀이 (0) | 2021.08.31 |
| 알고리즘 - 이진 탐색 알고리즘 (Binary Search algorithm) (0) | 2021.08.31 |