https://youtu.be/7C9RgOcvkvo?list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&t=2563

<문제1: 음료수 얼려 먹기>

- 연결 문제 찾기


<DFS를 이용해서 문제 해결하기>

#DFS로 특정 노드를 방문하고 연결된 모든 노드들도 방문
def DFS(x,y):
#주어진 범위를 벗어나는 경우에는 즉시 종료
if x<=-1 or x>=n or y<=-1 or y>=m:
return False
#현재 노드를 아직 방문하지 않았다면
if graph[x][y] == 0:
#해당 노드 방문 처리해주기
graph[x][y] = 1
#상하좌우 위치들도 모두 재귀적으로 호출
DFS(x-1, y)
DFS(x,y-1)
DFS(x+1, y)
DFS(x,y+1)
return True
return False
n,m = map(int,input().split())
#2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int,input())))
#모든 노드(위치)에 대해서 음료수 채우기
result = 0
for i in range(n):
for j in range(m):
#현재 위치에서DFS 수행
if DFS(i,j) == True:
result += 1
print(result)
#1. 해당 위치의 값이 0일 때, 방문처리를 해주고 dfs를 재귀해서 상하좌우의 위치들도 모두 노드 방문 처리를 해준다. 이때 상하좌우로 호출된 경우엔 리턴값으로 처리되지 않고 방문처리를 하기 위함이다! 결국 시작점 노드, 즉 해당 노드가방문처리가 되었다면 처음방문하는 곳에만 result 값을 증가시키는 구조로 진행된다.
#2. 2차원 리스트로 맵정보를 입력 받아준다.
#3. 이중 반복문을 통해서 nXm 행렬을 돌면서 True값이 반환된 경우 음료를 얼려먹을 수 있는 길이므로 result값을 +1 해준뒤 결과값인 result를 출력해주면 답이 나온다.
<문제2 미로 탈출>


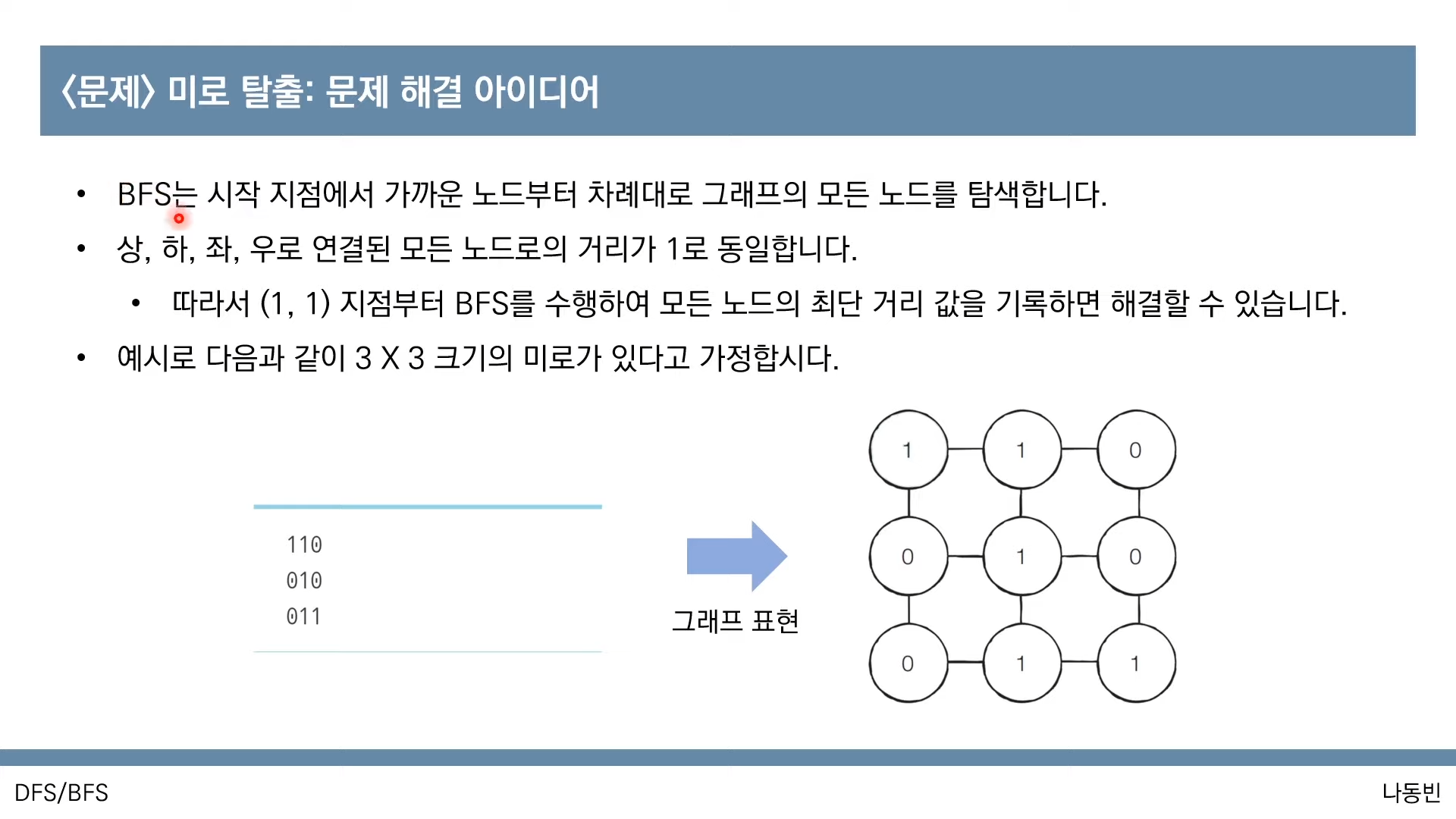
- BFS는 간선의 비용이 모두 같을 때 최단 거리를 구할 때 사용할 수 있는 알고리즘이다.
#DFS로 특정 노드를 방문하고 연결된 모든 노드들도 방문
def BFS(x,y):
#큐 구현을 위해 덱 라이브러리 사용
queue = deque()
queue.append((x,y))
#큐가 빌 때까지 반복하기
while queue:
x,y = queue.popleft()
#현재 위치에서 4가지 방향의 위치 확인
for i in range(4):
nx = x+dx[i]
ny = y+dy[i]
#미로 찾기의 공간을 벗어난 경우 무시
if nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
#괴물이 있어서 못가는 부분은(벽인 부분으로 생각) 무시
if graph[nx][ny] == 0:
continue
#해당 노드를 처음 방문하는 경우에만 최단 거리를 기록
if graph[nx][ny] == 1:
#직전 거리의 거리 값에 +1만큼 해준다.
graph[nx][ny] = graph[x][y] + 1
queue.append((nx,ny))
#가장 오른족 아래까지의 최단 거리를 반환해준다.
return graph[n-1][m-1]
from collections import deque
#BFS를 사용할 땐 큐를 이용하는 것이 좋고, 큐는 리스트를 사용하는 것보다 라이브러리를 사용해야 메모리 효율성이 좋다.
n,m = map(int,input().split())
#2차원 리스트의 맵 정보 입력 받기
graph = []
for i in range(n):
graph.append(list(map(int,input())))
#이동할 네 가지 방향을 정의해준다. (상,하,좌,우)
dx = [-1,1,0,0]
dy = [0,0,-1,1]
print(BFS(0,0))

'자료구조와 알고리즘 > 이것이 취업을 위한 코딩테스트다' 카테고리의 다른 글
| 알고리즘 - 정렬 알고리즘(sorting algorithm) 기초 문제 풀이 (0) | 2021.08.29 |
|---|---|
| 알고리즘 - 정렬 알고리즘(sorting algorithm) (0) | 2021.08.28 |
| 알고리즘 - BFS(Breadth-First Search) (0) | 2021.08.20 |
| 알고리즘 - DFS(Depth-First Search) (0) | 2021.08.20 |
| 알고리즘 - 재귀 함수(Recursive Function) (0) | 2021.08.20 |